bayesian classification
Bayesian Classification: Why?
•Probabilistic learning:
–Calculate explicit probabilities for hypothesis
–Among the most practical approaches to certain types of learning problems
•Incremental:
–Each training example can incrementally increase/decrease the probability that a hypothesis is correct.
–Prior knowledge can be combined with observed data.
•Probabilistic prediction:
–Predict multiple hypotheses, weighted by their probabilities
•Standard:
–Even when Bayesian methods are computationally intractable, they can provide a standard of optimal decision making against which other methods can be measured
Bayesian Theorem
•Given training data D, posteriori probability of a hypothesis h, P(h|D) follows the Bayes theorem
•MAP (maximum posteriori) hypothesis
•Practical difficulties:
–require initial knowledge of many probabilities
–significant computational cost
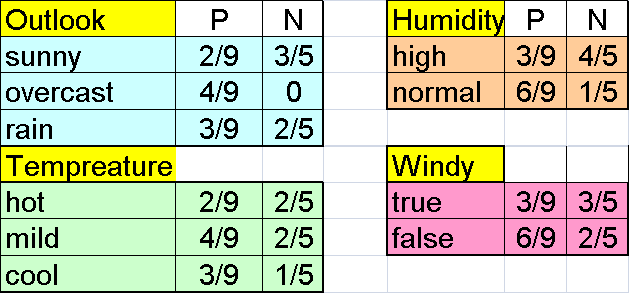
Naïve Bayes Classifier
•A simplified assumption: attributes are conditionally independent:
![]()
where V are the data samples, vi is the value of attribute i on the sample and Cj is the j-th class.
•Greatly reduces the computation cost, only count the class distribution.
Naive Bayesian Classifier
•Given a training set, we can compute the probabilities